The beer-brewing ratios of the Egyptian system.
The examination of Mesopotamian brewing ratios is based on hundreds of cuneiform tablets, day-to-day accounts of grains and brewing ingredients used to brew various grades of beer.
The study of Egyptian brewing ratios is based on two mathematical exercise papyri, the Ahmes/Rhind papyrus and the Golenichtchev or Moscow papyrus, tous deux datés du Moyen Empire, respectivement la XIIè (1991–1778 BC) et la XIè (2150-1991 BC) dynasties. These two documents list arithmetic, algebraic and geometric problems, 91 for the Ahmes/Rhind papyrus, 25 for the Moscow papyrus[1]. Only some of the arithmetic exercises concern the question of beer-brewing ratios: 10 for the Ahmes/Rhind papyrus, 10 for the Moscow papyrus.
They deal with ways of comparing (or barter) a given quantity of beer with an equivalent quantity of bread, and conversely. Or to convert a given volume of beer with one specific gravity into another volume of beer with a different specific gravity. Or to divide a volume of beer of a given strength among various people who are to receive beer of different quality (density) according to their social rank.
These calculations pursue an obvious practical purpose. The exercises are intended for the mental training of scribes who have to make such calculations on a daily basis in order to control the use of the grain brought out of the granaries. These grains are converted into malt (bcha, bš3  ), into beer (hnq.t
), into beer (hnq.t 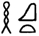 and variant
and variant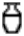 which also refers to the beer jar-dś) or bread (beer bread or baker's bread).
which also refers to the beer jar-dś) or bread (beer bread or baker's bread).
Calculating beverage rations from beer of various gravities (strength) is also the scribe's job. He must also know how to convert a number of loaves of bread of a given weight into a number of jars of beer of a given gravity on the basis of the volumes of grain used in both cases. Finally, he must recalculate the density of a beer contained in a jar after it has been diluted with water.
All these exercises are aimed at the practical management of the beer and bread rations allocated to the teams working in the workshops or in the fields. These daily or monthly food rations must respect the social rank of the recipients, as they do in Mesopotamia. A team leader does not receive the same amount of grain, in the form of beer and bread, as a simple labourer.
The arithmetical exercices given by the two papyrii known as "pefsu problems" have been analysed from the point of view of an Egyptian economy functioning thanks to exchanges in kind, a barter economy between producers of grains and royal institutions (palaces, temples, sanctuaries) or between these institutions themselves. The social side has been underestimated. Brewing ratios are more than brewers' recipes. They express the need to control the density of the beer wort in relation to the volumes of grain used. The volume of grain measures exactly how much grain is given to the recipients of the beer rations each day or month. This share varies according to their social status or their place in the hierarchy of a team of workers.
Calculating the density of a beer, the proportion of grain contained in a given volume of beer, guarantees the effective respect of social hierarchies, knowing that the whole of Egyptian society drinks beer, from the humblest worker to the pharaoh. In Egypt, the beer brewing ratios are the business of the scribes rather than that of the brewers.
WHAT ARE THE TOOLS OF THE EGYPTIAN SCRIBE?
To evaluate and calculate the density of beers, the Egyptian scribe needs three units: the hekat, which measures a volume of grain, the dś-jar, which gives a volume of beer, and the pefsu, which gives the mathematical relationship between these two values.
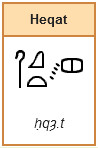
The hekat (or heqat) is the Egyptian unit of volume used to gauge quantities of grain or beer. It is worth 4.8 litres. The hekat is the volume of grain that a shovel can pick up from threshing floors or granaries. This reference-unit follows all operations related to grain: storage, flow, exchange and especially processing into bread or beer. The hekat measures volumes of raw grain (barley, starch wheat), malt, flour, etc.[2].
ds Faulkner p. 316, Wb. V p. 485, 3-15
-
cf. W22![D46 [d] d](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_D46.png)
![O34 [z] z](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_O34.png)

1 hekat = 3,75 kg or 4,8 litres.
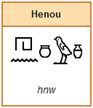
1 hekat = 10 hin (henou)
1 hekat = 64 dja
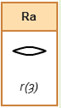
1 hekat = 320 ro (ra)
The dś-jar ( or jug for beer W22) is a jar with a standardised capacity. Without this known fixed volume, measuring the densities of beer would remain a theoretical calculation. Similarly, the problems of diluting beer with water, or mixing barley and dates to brew it, exercises proposed by the Ahmes/Rhind papyrus or the Moscow papyrus, would have no practical application[3].
Knowing the capacity(ies) of the dś-jar remains the crucial question. Without this data, the actual density of Egyptian beers cannot be estimated. Wolfgang Helck proposed in 1971 a capacity between 2.5 and 3 litres[4].
An example of a beer jar with clay stopper (h. 30 cm diam. sealing 10.5 cm) dated to the 12th dynasty (reign of Amenemhat I) comes from Thebes, Southern Asasif, Tomb of Wah. This beer jar is contemporary to the sources and knowledges that gave rise to the two papyri (Middle-Empire ca. 1981-1975 B.C.). It contains about 8 litres[5].A capacity of between 5 and 8 litres is incompatible with a standardised jar, at least in order to ensure that the wort density matches the very precise calculations done by the scribes (see below). The beer jars used in Egyptian breweries have a larger capacity, about 30 litres (Jar found in the funerary temple of Amenemhet III, Dashur).
The dś-jar is also used to collect date juice after pressing. It can hold 20 hin, or about 10 litres[6].
The issue of the capacity of the dś-jar is therefore unresolved. Publications refer to jugs (0.5 litres), jars (5 litres) and archaeologists have discovered dś-jar (8 litres). These beer containers evolved over three millennia. They also varied from one region to another. Alongside the dś-jar, the ḏwjw (djouiou) beer jar also served as a measure for beer. There was probably a standardised range of dś-jars: small, medium and large dś-jars, as well as for the ḏwjw-jar. The jars specimens and textual references to the ds-jar mostly come from funerary contexts (tombs and stereotyped offering list forms). Less is known about the contexts related to the distribution of beer rations.
psw Faulkner p. 94, Wb. I p. 552, 8-11
The pefsu (or pesu, pfśw) measures the beer gravity, specifically the theorical density (sugars) of the wort before its fermentation.
Pefsu = number of dś-jars of beer / number of hekat of grain.
10 dś-jars of beer brewed with 5 hekat of grain = 2 pefsu. 10 dś-jars of beer brewed with 10 hekat of grain = 1 pefsu. The higher the pefsu, the lower the gravity of the beer. The pefsu is also a unit of practical use, not just a theoretical value. Beer offerings or forms dedicated to the care of people after death state the number of dś-jars of a given pefsu[7].
In practice, the pefsu, the theoretical beer brewing ratio, has very different values. W. Helck retains the pefsu values of 1, 1½ and 2 as being in common use in the documents emanating from the temples and royal houses. He points out, however, that ratios 2, 3, 4, 5, 10, 14, 20, 30, 40, 50, are attested during the New Kingdom (Helck 1971, 47). A pefsu of 50 (1 hekat of grain for 50 dś-jars!) produces an extremely weak and waterly beer, regardless of the volume of a dś-jar. Conversely, a pefsu 1 is indicative of a very strong beer.
One fact is clear. Beer brewing ratios were implemented in ancient Egypt to enforce a social hierarchy. The lower the pefsu, the higher the rank of the beneficiary. The arithmetic exercises proposed to the scribes by the Ahmes/Rhind papyrus demonstrate this link between beer gravity and the social rank of the recipient (see below, in particular n° 65)[8] .
THE AHMES/RHIND PAPYRUS AND THE GRAVITY OF BEER.
Problem 65 distributes 100 loaves of bread among a team of 10 men. The team leader, the watchman and the boatman receive double rations. Here it is a question of bread, elsewhere of beer. The rations take into account the hierarchy within the team. The position in this hierarchy is measured in terms of the volume of grain contained in the bread and beer rations: more or less heavy bread, more or less strong beer.
Ahmes/Rhind problem 65: distribute 100 loaves of bread among a team of 10 men.
Example of dividing 100 loaves among 10 men, including a boatman, a foreman, and a door-keeper, who receive double portions. What is the share of each?
The working out. Add to the number of the men 3 [for those with double portions]; it makes 13. Multiply 13 so as to get 100; the result is 7 2/3 1/39. This is the ‘eating’ [ration] for seven of the men, the boatman, the foreman, and the door-keeper receiving double [portions].
For proof we add 7 2/3 1/39 taken 7 times and 7 2/3 1/39 taken 3 times for the boatman, the foreman, and the door-keeper. The total is 100.
The number of loaves can be increased according to the hierarchical position of the recipients. The number of beer jars can also be increased. However, the beer-related pefsu calculation exercises show that the scribe will also play on the gravity of the beer: more or less grains for the same volume of beer, dilution with water, addition of dates and even partial replacement of barley by other cereals such as emmer-wheat.
The dilution of beer is a practical solution to adapt its gravity to the social rank of the recipient. Problem 71 shows how to calculate the pefsu, the theoretical gravity, of a diluted beer.
Ahmes/Rhind problem 71: dilution of the beer.
From 1 dś-jar of beer, 1/4 has been poured off, and then the jar has been filled up with water. What is the pefsu of the diluted beer?
Reckon the amount of malt (besha) in 1 dś-jar of beer; it is ½ hekat. Take away 1/4 of it, namely 1/8 hekat; the remainder is 1/4 1/8 hekat. Multiply 1/4 1/8 hekat so as to get 1 hekat; the result is 22/3 and this is the pefsu.
The solution given by Ahmes is very insightful. We don't know the initial pefsu of the beer in the dś-jar. However, Ahmes tells us "Reckon the amount of malt (besha) in 1 dś-jar of beer; it is 1/2 hekat". In the proposed exercise, the dś-jar of beer before dilution was worth 2 pefsu (1/0.5). Diluting it by a quarter is like brewing it with only 1/4 1/8 of the original half-hekat. The ratio of 1/4 1/8 to 1 hekat is indeed 2 2/3 (1/0.375 = 2.66666... in our decimal system).
Initially, the dś-jar contains beer of pefsu=2, brewed with ½ hekat of malt, that is 2.4 litres or 1.8 kg of malt. If we assume that this pefsu=2 corresponds to a technical ratio of 1:1 (the actual ratio between the initial volume of malt and the volume of brewed wort), then the dś-jar contains about 2.4 litres. This technical ratio (actual gravity of the wort before fermentation) corresponds to a strong beer (see Mesopotamian beer ratios).
Pefsu 1 beers are twice as strong and probably reserved for the top of the Egyptian social hierarchy. Pefsu 1 seems to be the highest beer gravity found in Egyptian documents.
Problem 77 documents another practical case, that of exchanging beer jars for breads with the same pefsu. In other words, on the basis of the same volume of grain used to make them. The 'value' of rations is calculated on the volume of grain, a social logic that applies to teams of ration-holders but also between people of different social rank. In theory, a person can receive only beer or only bread, as long as the total amount of grain used matches his or her social rank.
Ahmes/Rhind problem 77 : exchange beer jars for breads.
10 jars of beer pefsu 2, are to be evenly exchanged for aHa (x) loaves of bread pefsu 5. Find aHa. aHa = 25. Reckon the amount of wedyet-flour in 10 ds-jars of beer; it is 5 hekat. Multiply 5 by 5; it makes 25. Say then that it takes 25 loaves to make the barter.
It takes 5 hekat of malt to brew 10 jar-ds of beer pefsu 2.
5 hekat of bread pefsu 5 => 25 loaves of bread.
Is beer made in Egypt from wedyet-flour? Probably if it is used to make beer loaves which are then crumbled for brewing. Note that in the calculation of the pefsu, raw grain, malt and flour are equivalent.
W. Helck has pointed out that the Egyptians knew how to remove 1/31 of the volume after milling the grains (Helck 1971, 44). A beer with a pefu calculated on an initial volume of malt is therefore richer than one calculated on a volume of raw grain. Malting causes the raw whole grain to lose about 20% of its volume. The same applies to the use of flour (1/31th ≈ 3%).
Problem 78 documents the reverse case of 77: bartering bread for beer jars with equal pefsu. Ahmes introduces in his statement the aHa, the unknown value to be calculated, the equivalent of the unknown x in our algebraic equations.
Ahmès/Rhind problem 78 : exchange of breads for beer jars.
100 loaves of pefsu 10 must be bartered evenly for aHa dś-jar of beer pefsu 2. Find aHa. aHa = 20 dś-jars of beer.
Reckon the amount of wedyet-flour in 100 loaves of pefsu 10; it is 10 hekat. Multiply 10 by 2; it makes 20. Say then that it takes 20 dś-(jars) of beer to make the exchange.
THE MOSCOW PAPYRUS AND THE GRAVITY OF BEER.
The Moscow papyrus offers similar exercises. 10 out of 21 exercises are pefsu problems. Among them, nos. 5, 8, 9, 20 calculate the pefsu of loaves of bread, 12, 13, 14 and 16 the pefsu of beer jars, 22 and 24 equivalences between loaves of bread and beer jars of different pefsu[9].
Problems 9 and 13 are similar to Ahmes/Rhind 71:
Moscow problem 13 : dilution of the beer.
Given a jar-ds of 2 pefsu, what will the pefsu be after diluting a quarter of the beer?
Answer: the beer required 1/2 hekat of grain minus 1/4 (replaced by water) = 3/8, the new pefsu value = 8/3.
Problems 22 and 24 allocate barley for making bread and beer, the two basic staples of Egyptian food rations:
Moscow problem 22 : barley to make bread and beer.
10 hekat of Upper Egypt barley to make 100 loaves of bread and 10 ds-jugs of beer pefsu 2. Find the pefsu of bread.
10 ds-jars of beer pefsu 2 = 5 hekat. 10–5 hekat for100 loaves => pefsu = 20.
Moscow problem 24 : barley to make bread and beer.
15 hekat of Upper Egypt barley to make 200 loaves of bread and 10 ds-jugs of beer. The pefsu of the beer is 1/10 that of the bread. Find the pefsu of beer and that of bread.
200 loaves pefsu 20, 10 ds-jugs of beer pefsu 2.
Problem 16 deals with the replacement of barley (or barley malt) by emmer-wheat. The formula "3/4 n bš3 bnr"[10], literally 3/4 times malt for (1/4) dates, describes the composition of a type of beer and can be used in the calculations. Some problems take this into account and decrease by 1/4 volume of grain needed (alike the beer dilution case), others ignore it to calculate the new pefsu. Here the ratio of barley to emmer-wheat = 22/3. A dś-jar of pefsu 2 beer brewed with ½ hekat of barley becomes a beer pefsu 2 brewed with 0.375 hekat of emmer-wheat. This means a dś-jar filled with barley beer pefsu 2 can be bartered for 0.375 hekat of emmer, or a dś-jar of beer brewed with it.
Moscow problem 16 : beer bartered for emmer-wheat.
A ds-jug of beer pefsu 2 in exchange of emmer at the value 22/3. Find the emmer.
1 ds-jug of beer pefsu 2 (1/2 hekat) exchanged for 3/8 hekat of emmer.
Problem 12 is one of the most interesting. It is similar to Ahmes/Rhind 71 or Moscow 13 (beer dilution), but this time the beer is brewed with equal parts of malt and dates. The calculation of the final theoretical gravity is a little more complicated and involves a gravity ratio between the barley and the mixture malt-dates.
Moscow problem 12 : beer half malt, half dates.
13 hekat of Upper Egyptian barley to make 18 jars of half-malt half-date beer (bš3 mì bnr), idem malt [same qty 13 hekat] dates pefsu 21/6. Final pefsu of the beer = 3. Why?
Answer: the malt-date mixture is worth 6 hekat (13 hekat of barley / pefsu 21/6 = 6). So 18 jars/6 hekat-equivalent- malt-dates = 3 pefsu.
These last two problems show the practical limitations of the Egyptian system. As soon as the beer is brewed with heterogeneous ingredients, additional information is required. They will say, for example, that the malt is 22/3 of the emmer (prob. 16), or that the ratio of barley to a mixture half-malt half-dates is 21/6 (prob. 12).
Where do these last two ratios come from? The pefsu calculations do not take into account the manufacturing process (time, labour, materials), nor the quality of the ingredients (barley and barley malt are equivalent). Only the nature of the raw materials is taken into account, hence the ratios between barley, wheat and dates. Charles Nims (1957) interpreted these proportions as trade scales or conventional values for barter. This explanation is not incompatible with a social logic of brewing ratios based upon the equivalence of grain volume (beer and bread) ⇔ social rank. Beers brewed partly with dates require an additional ratio to compare a volume of dates and a volume of barley and reduce the pefsu to a theoretical volume of grain.
SOCIAL STATUS GRIDS ⇔ BREWING RATIOS (PEFSU).
Ostracon from Deir el-Medineh. workmen's register, 280 days of attendance at work, including beer brewing. Year 40 of Ramses II (r. 1279-1213 BC), verso BM EA5634.
Year 40 of Ramses II (r. 1279-1213 BC), verso BM EA5634.
Many lists of ration distributions illustrate the equivalence between social status and food benefits. The proportionality is quantitative: more loaves of bread and jars of beer per person for the royal entourage of the palace or the heads of the sanctuary, for example, than for the porter or the menial servant (Helck 1971, 55-62).
To our knowledge, we do not have any texts on the distribution of rations in Egypt that illustrate a qualitative equivalence. For example, a higher beer gravity (pefsu 1) for the top of the hierarchy and a lower one (pefsu 2 to 4 or even less) for the lowest.
The very low pefsu values (20, 30, 40, ...) reported by (Helck 1971, 49) are attested to along the New Kingdom and used during collective celebrations gathering a large number of people. Brewing a large quantity of beer then probably means drastically reducing its gravity.
The site of Deir el-Medina, near Thebes, was the location of a village of workers specialised in the construction and maintenance of New Kingdom necropolises (c. 1550 BC-c. 1077 BC). Archaeologists have found ration accounts written on pieces of limestone, pottery shards or papyrus. The monthly grain rations (emmer + barley) clearly show differences in status[11].
| Emmer and barley rations (litres) for the teams working at Deir el-Medineh, afer Janssen 1997, 14-15. | ||||
| Emmer | Barley | Monthly | Daily | |
| Foreman, scribe | 528 | 192 | 720 | 24 |
| Worker | 384 | 144 | 528 | 17,6 |
| Guard | 312 | 120 | 432 | 14,4 |
| Slave woman | 144 | 144 | 288 | 9,6 |
| Young men | 144 | 48 | 192 | 6,4 |
| Doorkeeper | 96 | 48 | 144 | 4,8 |
| Doctor | 96 | 24 | 120 | 4 |
These rations feed not only the incumbent but also his family who live on site. The grain is used to make bread and brew beer. In view of the differences in volume between the team leader + scribe and the workers, the surplus of grain (+40%) allocated to the former allowed them to brew stronger beers. Some ostraca from Deir el-Medineh tell of days of absence for brewing beer followed by binges (Janssen 1980, SAK 8. Grandet 2002, cat. 113). Unfortunately we have no information on the strength or gravity of these beers.
A COMPARISON WITH MESOPOTAMIAN BREWING RATIOS.
Faced with the same situation, the massive production of beer controlled by central grain storehouses and beer brewing workshops, the Mesopotamian scribe adopts a similar approach: controlling only the inputs and outputs. He only counts the grains that enter the brewery and the jars of beer that leave it.
The Egyptian scribe created the pefsu, a theoretical unit equal to the number of loaves or jars of beer obtained with 1 hekat of grain. His formula is: x jars (or x loaves) /y hekat = z pesu. It therefore works like most Mesopotamian ratios (½ ta beer, 1 ta, 1½ ta, 2 ta, ...) and is based, like them, on the standardisation of the size of the loaves or the capacity of the jars: the Egyptian dś-jar and the Mesopotamian piḫum-jar (or dida-jar).
However, there is a difference between the Egyptian pesu and the Mesopotamian beer brewing ratio.
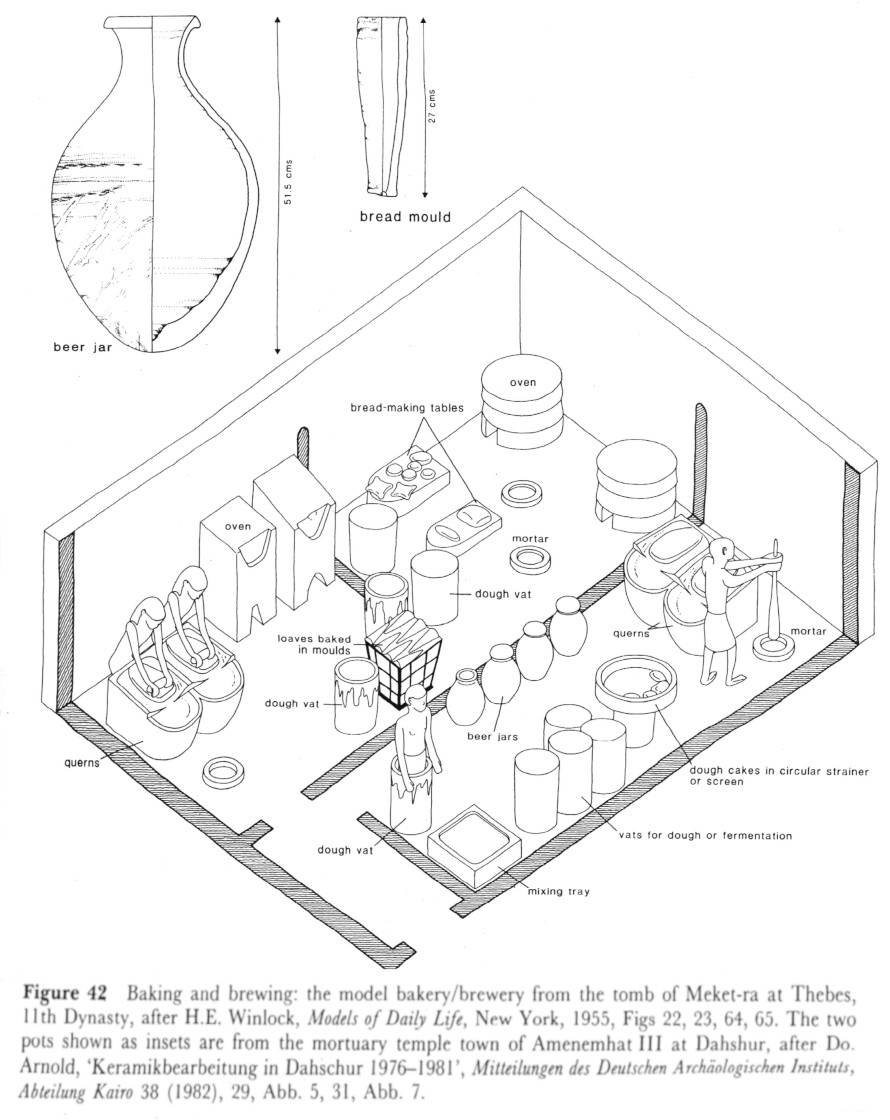 Baking and brewing wooden model (Kemp fig. 42 after Winlock 1955). Beer jar (above).
Baking and brewing wooden model (Kemp fig. 42 after Winlock 1955). Beer jar (above).The latter does not reach the practical and theoretical generality of the former. The Egyptian scribe used the pesu to convert and compare all grain-based products (bread, cakes, malt, beer), but also dates and other foods such as oil or fat. The pesu is also used as a real unit of calculation in mathematical exercises for apprentice scribes.
Nevertheless, the actual management of each type of beer is based on conventional ratings, but also on actual checks in the field.
Was this the reason that prevented the pragmatic Mesopotamian manager from forging his theoretical unit of calculation for beer?
Egyptian and Mesopotamian brewery managers provide a different solution to the same problem. It would be interesting to know the reasons that governed these choices. The Egyptian pesu finds its practical application in barter. A dś-jar of 1 pesu is exchanged for 1 pesu of other products and according to defined scales: 3/8 hekat of emmer-wheat, 2/3 of dates, 3/2 of malt or 1 pesu of loaves.
Did too great a variety of beers inhibit equivalent modes of calculation in Mesopotamia? The notations 1 (jar)-piḫum or 1 (jar)-dida imply their barley equivalents in the mind of the Mesopotamian administrator, but the information remains implicit and dependent in all cases on each type of beer, known only to the one who has the jar in hand. As for the exchange of beer jars for other products, it is based on common scales known to all. They all relate to the volume of barley, the reference commodity. There is no need to establish a theoretical unit of exchange. The great Mesopotamian merchants proceeded in the same way and converted the value of a commodity into barley, silver or tin in the North. There was no need for an abstract unit of reference like the Egyptian pesu, which was the practice of the scribes.
Model of a brewhouse. 13 workers grinding, 9 sifting flour, 4 crouching in front of ovens, 3 brewing mash in vats, one overseer. Wooden model of a brewing workshop, Thebes, 11th Dynasty, BM EA40915.
Wooden model of a brewing workshop, Thebes, 11th Dynasty, BM EA40915.
Besides the scribal habits, there is the practice of the brewer. He only has the usual equipment - baskets, pots, jugs, vats or more or less standardised containers - to measure his raw materials, the wort and the finished beer. Standardised utensils, pragmatism and a predefined recipe save the brewer from precise measurements and learned calculations, two techniques that are practically out of his reach[12].
This brewing method implies that there is only one quality or gravity of beer for each brew.
For the brewer, a brew is the minimum unit of work, the process by which he commits this volume of grain to produce such or such a volume of beer of a defined quality. The same pouring of grain and ingredients does not produce a superior beer and a diluted beer obtained by washing the spent grains, as has sometimes been assumed. This would require the brewer to make complex calculations to break down the initial volume of grain into a double output of two beers with different ratios. This would force him to take lessons from his Egyptian colleague in handling the pesu (see beer dilution problems)!
This is why Mesopotamian accounting records always match a given volume of grain with a given final volume of a single quality of beer, so as not to deviate from the logic of the beer brewing ratio. The Egyptian brewer, or scribe, on the other hand, seems to be able to dilute the wort to obtain a lower gravity, the pefsu value of which he knows how to calculate.
BIBLIOGRAPHY
Chace Buffum Arnold, Ludlow Bull, Henry Parker Manning, The Rhind Mathematical Papyrus. Volume I, 1927. archive.org/details/arnoldbuffumchaceludlowbullhenryparkermanningtherhindmathematicalpapyrus.volumei
Clagett Marschall, Ancient Egyptian Science. A Source Book. Volume Three. Ancient Egyptian Mathematics. 1999. books.google.fr/books?id=8c10QYoGa4UC&pg=PA60&lpg=PA60&dq=pefsu...
Grandet Pierre, Les artistes de Pharaon. Deir el-Medineh et la Vallée des Rois (Catalogue exposition du Louvre 2002).
Grandet Pierre, Le Papyrus Harris I (BM 9999) 1-2, Bibliothèque d'Etude (Publication de l'IFAO) = BdE 109/2, 1994.
Helck Wolfgang, Das Bier im Alten Ägypten, Gesellschaft für die Geschichte und Bibliographie des Brauwesens E.V., Berlin 1971. Helck 1971
Janssen Jac, Village Varia. Ten Studies on the History and Administration of Deir el-Medina, Nederlands Insituut voor het Nabije Oosten, Leiden 1997.
Janssen Jac, Absence from work by the necropolis workmen of Thebes. Studien zur Altägyptischen Kultur (SAK 8), 1980, 127-152.
Kemp Barry J. , Ancient Egypt. Anatomy of a civilization. Routledge 1989 (réimp. 1991). archive.org/details/BarryJ.KempAncientEgyptAnatomyOfACivilibOk.org
Nims Charles, The bread and beer problems of the Moscow mathematical papyrus, Journal of Egytian Archaeology 44, 1958, 56-65. jstor.org/stable/3855065
Powel Marvin, Ancient Mesopotamian Weight Metrology: Methods, Problems and Perspectives, in Studies in Honor of Tom B. Jones, Alter Orient und Altes Testament 203, 1979, 71-110
Robbins G. & Shute C., The Rhind Mathematical Papyrus: an ancient Egyptian Text, 1987, 50-52.
Spalinger Anthony, Dates in ancient Egypt, (Studien zur Altägyptischen Kultur 15), 263-267. jstor.org/stable/44324591
Struve Vasiliĭ Vasilʹevich, Mathematischer Papyrus des Staatlichen Museums der schönen Künste in Moskau. in Quellen und studien zur gescichte der mathematik, abt. A: Quellen. bd. 1. 1930.
NOTES
[1] 20 problems if we exclude unreadable exercises and merge 3 pairs of very similar exercises.
[2] On the units hekat and pefsu, B. Kemp "Ancient Egypt", 123-126. And the logic of rations ibid. 117-120. B. Kemp discusses on p. 124 the required standardisation of beer jars: "Many ration lists have survived. They tend to ignore pefsu values. They assume standardised beer jugs, and different kinds of bread can be grouped together as 'mixed' loaves. This assumes standardisation, a reasonable step in thinking in view of the scale and ubiquity of operations, in which those involved, including the potters making beer jugs, would naturally tend to produce standardised forms from a lifetime of practice." B. Kemp describes how rations change in quantity according to social rank (pp. 125-126) - number of loaves or jars of beer. He does not expect that beer rations can also vary according to the gravity of the drink. This technique solves a biological problem: a person cannot drink whole jugs of beer in proportion to his social rank!
[3] The utilitarian character of Egyptian mathematics is not always emphasised by Egyptologists who analyse its formulae from the point of view of the history of mathematics and compare it to Greek mathematics. The studies of the Ahmes/Rhind papyrus focus almost exclusively on geometry and algebra. The arithmetic of the so-called "pesu" or "pefsu" problems is considered too elementary. The publication in German of the Moscow papyrus by V.V. Struve in 1930, prepared by a study undertaken by Touraev in 1912-1920, reconstructed the text and added a translation with a detailed philological and mathematical commentary. The publication testified to the important theoretical scientific knowledge of the Egyptians, anticipating the achievements of Greek science (Struve's biography).
[4] Helck Wolfgang, Das Bier im Alten Ägypten, 1971. pp. 43-51 « Stärke und Arten des altägyptischen Bieres“, and especially p. 46. See also pp. 22-23 why bcha (bš3) refers to malt (and not a "flour or some kind of grain with fruits"!). Ultimately, one must refer to the scientific analysis done by Delwen Samuel with of beer remains retrieved from Armana-Egypt.
[5] Capacity of an ovoid jar = averageR2 * H * 3.14. Average radius = 9,25 cm. 9,25 * 9,25 * 30 * 3,14 = 8.060 cm3. Reference of the beer jar Met 20.3.256a–c. www.metmuseum.org/art/collection/search/572197
[6] Grandet Pierre, Le Papyrus Harris I (BM 9999) 1-2, BdE 109/2, 1994, p. 80.
[7] On the hekat and pesu units, B. Kemp, "Ancient Egypt", 123-126.
[8] Problem statement according to Arnold Buffum Chace, Ludlow Bull, Henry Parker Manning, The Rhind Mathematical Papyrus. Volume I, 1927.
[9] Charles Nims (1958) only counts 20 problems because 1 and 2 are illegible, 8 and 9 are combined, as well as 11-12, and 15-16.
[10] Charles Nims, The Bread and Beer Problems of the Moscow Mathematical Papyrus, JEA 44, 1958, pp. 56-59. The scribes discriminate between barley and emmer with the colour of the ink, barley drawn in black, emmer in red.
[11] The foreman and the scribe each receive 5½ khar (1 khar=96 l.) of emmer and 2 of barley / month, each labourer 4 + 1½, young man 1½ + 1, guard 3¼ + 1¼, porter 1 + ½, doctor 1 + ¼, slave woman 1½ + 1½ (Janssen Jac, 1997, 13-15).
[12] Powell (1979, 88-89) has shown the gap between common Mesopotamian technical and commercial practices using weights and measures on the one hand, and the extraordinary development of Babylonian mathematics on the other, which were dedicated to abstract computational problems (accounting, astronomy, conversion of units of measurement, school exercises).




![S29 [s] s](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_S29.png)
![Z4 [y] y](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_Z4.png)


![Q3 [p] p](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_Q3.png)
![I9 [f] f](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_I9.png)
![G43 [w] w](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_G43.png)


